Lossles Compression:
- Lossless compression is a class of data compression algorithms that allows the original data to be perfectly reconstructed from the compressed data. Lossless compression methods are reversible. Examples of lossless compression include GZIP, Brotli, WebP, and PNG.
- Lossles Compression is preffered for text file compression, while Lossy Compression is generally preferred
for audio, video and image files.
- File formats like ZIP use Lossless compression, while formats like MP3 and JPEG use
Lossy compression
- Data compression ratio , also known as compression power, is a measurement of the relative reduction
in size of data representation produced by a data compression algorithm. It is typically expressed as the
division of uncompressed size by compressed size. Thus, a representation that compresses a file's storage
size from 10 MB to 2 MB has a compression ratio of 10/2 = 5
Greedy Algorithm:
- Greedy is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit. Greedy algorithms are used for optimization problems.
- 1) Kruskal’s Minimum Spanning Tree (MST): In Kruskal’s algorithm, we create an MST by picking edges one by one. The Greedy Choice is to pick the smallest weight edge that doesn’t cause a cycle in the MST constructed so far
- 2) Prim’s Minimum Spanning Tree: In Prim’s algorithm also, we create a MST by picking edges one by one. We maintain two sets: a set of the vertices already included in MST and the set of the vertices not yet included. The Greedy Choice is to pick the smallest weight edge that connects the two sets
- 3) Dijkstra’s Shortest Path: Dijkstra’s algorithm is very similar to Prim’s algorithm. The shortest-path tree is built up, edge by edge. We maintain two sets: a set of the vertices already included in the tree and a set of the vertices not yet included. The Greedy Choice is to pick the edge that connects the two sets and is on the smallest weight path from the source to the set that contains not yet included vertices
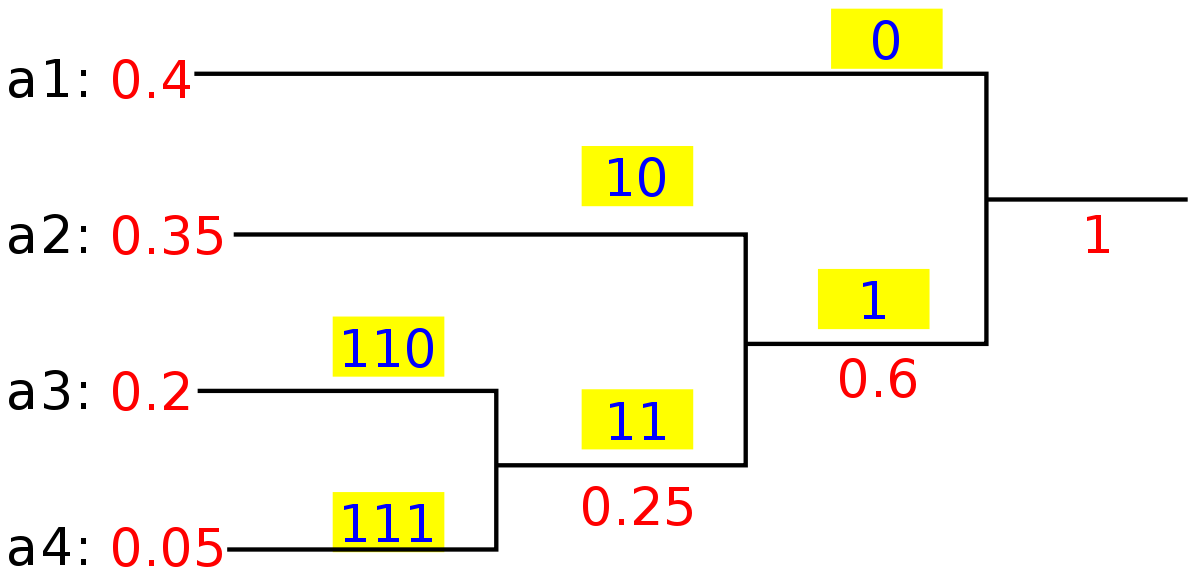
- 4) Huffman Coding: Huffman Coding is a loss-less compression technique. It assigns variable-length bit codes to different characters. The Greedy Choice is to assign the least bit length code to the most frequent character. The greedy algorithms are sometimes also used to get an approximation for Hard optimization problems. For example, Traveling Salesman Problem is an NP-Hard problem. A Greedy choice for this problem is to pick the nearest unvisited city from the current city at every step. These solutions don’t always produce the best optimal solution but can be used to get an approximately optimal solution. Here let us see one such problem that can be solved using Greedy algorithm
- Following are some standard algorithms that are Greedy algorithms:
Huffman Code:
-
A Huffman code is a particular type of optimal prefix code that is commonly used for lossless data
compression. The process of finding or using such a code proceeds by means of Huffman coding, an algorithm
developed by David A. Huffman.
-
The output from Huffman's algorithm can be viewed as a variable-length code table
for encoding a source symbol (such as a character in a file). The algorithm derives this table from the
estimated probability or frequency of occurrence (weight) for each possible value of the source symbol.
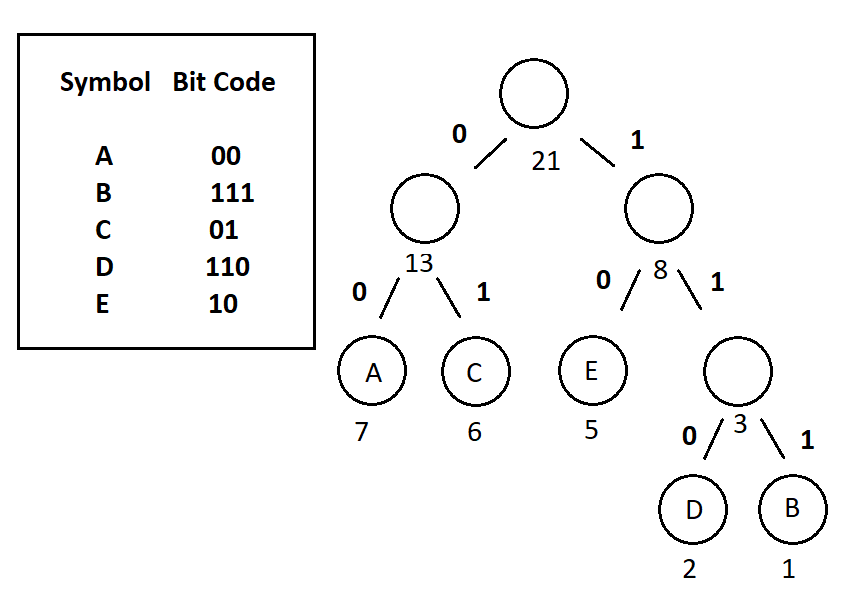
- Prefix Codes, means the codes (bit sequences) are assigned in such a way that the code assigned to
one character is not the prefix of code assigned to any other character. This is how Huffman Coding makes
sure that there is no ambiguity when decoding the generated bitstream.
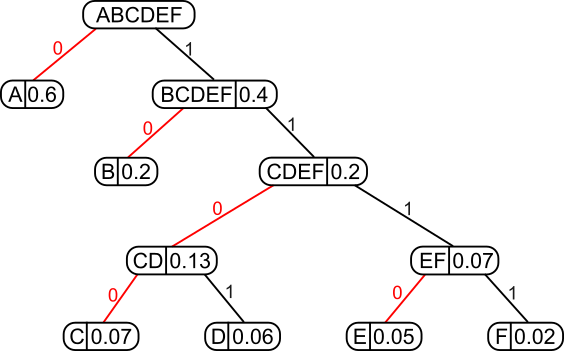
A Huffman coding tree built from this character frequency table: A=0.6, B=0.2, C=0.07, D=0.06, E=0.05, F=0.02.
Compression:
- Probability Calculation & Ordering the Symbols
- Binary Tree Transformation
- Assigning Codes to the Symbols
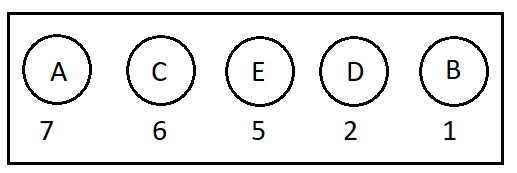
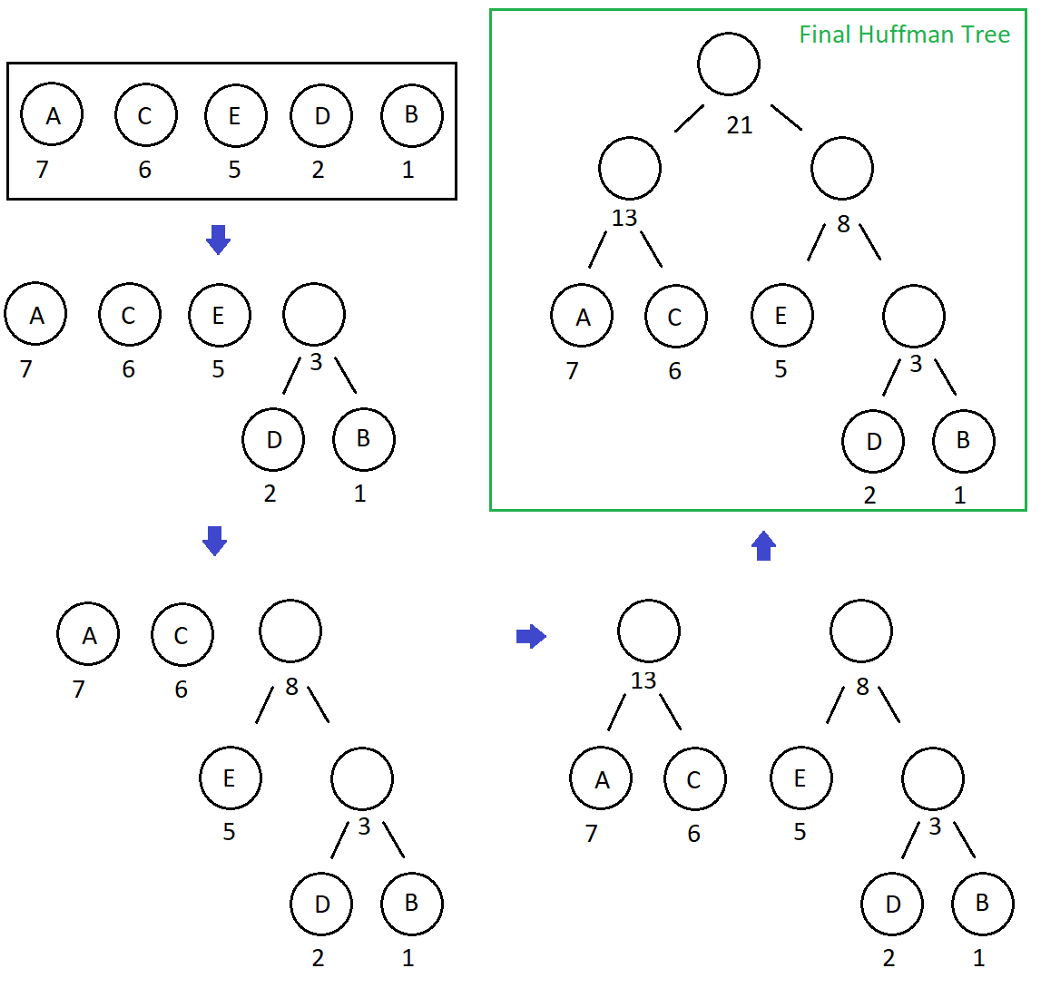
- 1. From the collection, we pick out the two nodes with the smallest sum of probabilities and combine them into a new tree whose root has the probability equal to that sum.
- 2. We add the new tree back into the collection.
- 3. We repeat this process until one tree encompassing all the input probabilities has been constructed.
- Having our Binary Huffman Tree obtained during encode phase, decoding is a very simple process to perform.
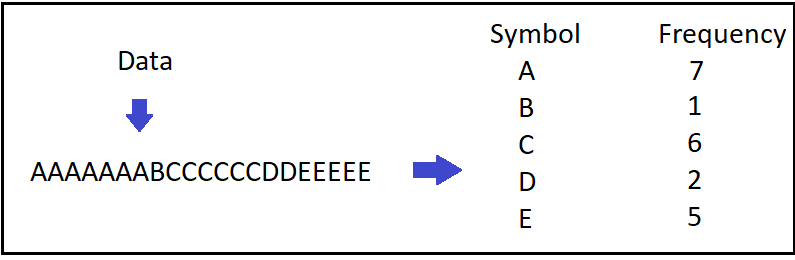
- Let’s consider we have the same example with Huffman Encoding post, therefore we have AAAAAAABCCCCCCDDEEEEE as our initial data and 000000000000001110101010101011101101010101010 as encoded output with the following Huffman Tree:
- Now the only thing we should do is starting from the head of Huffman Tree and from the beginning of the encoded data, each time we encounter 1 we go right and while we encounter 0, we go left through the Huffman Tree. When we reach at a leaf node, we obtain the symbol! Then we just start again from the head of Huffman Tree while moving forward on encoded data.
- Data compression is a topic of many applications and it has various different types of algorithms beside of “frequency based” Huffman Algorithm. You can check for “dictionary based” methods like LZ77 LZ78 LZW which are useful for image compression especially.
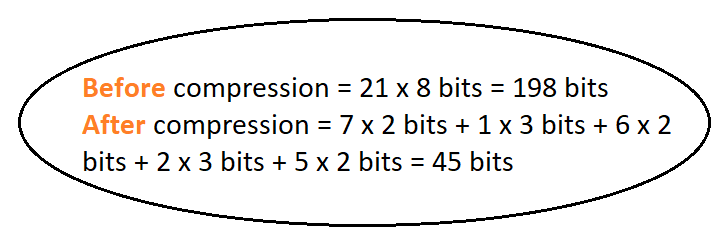
- As a conclusion, we see that the compression ratio does not change with the growing amount of data, and this ratio is close to 2:1. We can say that Huffman Encoding is an algorithm that compresses the data to its half size. Although it is old, it is still an effective compression algorithm!
De-compression:

